You say: "For any event P (where P is a label for something happening at a given place at a given time), the events within P's future light cone make up its absolute future and those within its past light cone make up its absolute past: the former are the events that P can influence and the latter are the events that can influence P." So as I understood this, it means every two events that are causally connected, must lie in each others light cones (if event A causes event B, then B is in A's future cone and A int B's past cone).
Yes, I may have been a little sloppy there. The idea that light cones are about the causal structure of spacetime is deeply engrained in physicists. Let me have another try being more careful. We're really interested in five sets of events related to a given event P:
- Events which occur before P according to all observers.
- Events which occur at the same time as P according to all observers.
- Events which occur after P according to all observers.
- Events which can influence P.
- Events which P can influence.
In classical, Newtonian physics the situation is easy and intuitive. Sets 1 and 4 are the same, and are the past of P. Sets 3 and 5 are the same, and are the future of P. There's a non-empty set 2, which is the "present" of P. All events other than P fall into one of these three classes. Signals that are as fast as you like don't change this.
In special relativity without faster-than-light signals things are a little more complicated. Sets 1 and 4 are the same, and are the absolute past of P. Sets 3 and 5 are the same, and are the absolute future of P. (People sometimes talk about the "chronological" and "causal" pasts and futures of an event but the use of the word "causal" used in that way would make things even more confusing!) Set 2, though, is empty: there are no other events that all observers agree happen at the same time as P. There is, instead, a large region of spacetime which is not in any of the five sets: events that can't influence or be influenced by P, and don't take place absolutely before, at the same time as or later than P.
In special relativity with faster-than-light signals, sets 1 and 4 are no longer the same, and nor are 3 and 5. Sets 1, 2 and 3 are still the same as in the case without faster-than-light signals. The Lorentz transformations only rely on the principle of relativity and the invariance of the speed of light and so faster-than-light signaling doesn't change the temporal ordering of pairs of events within each others' light cones. However, it's fairly easy to see that with FTL signals the sets 4 and 5 become the whole of spacetime! Events in P's absolute past can influence P anyway. Events outside P's absolute past or future can influence P via superluminal signals in appropriately chosen frames. Events in P's absolute future can influence P through the construction shown in figure 5 (although there it's an event in R's absolute future affecting R.) Causality is quite hard to define at the best of times[1] but if any other event can influence an event P then clearly we're very far away from being able to give a conventional description of causal relationships between events.
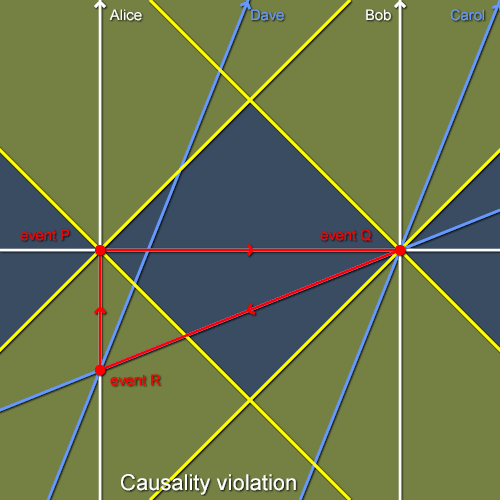
This is the thing that has always confused me and still keeps on doing so. What I would like to see, is the second half of this example: This first half makes assumption that light speed cannot be exceeded (light cones themselves make that assumption), so if this assumption is false, outcome is not reliable. So if someone could prove that FTL implies time travel with assumption that FTL is possible, then we could safely assume that FTL implies time travel.
I don't think it's strictly true that special relativity assumes that light speed cannot be exceeded. Instead it postulates that the speed of light is invariant. Relativistic dynamics then prevent any object that is moving more slowly than light being accelerated to the speed of light or faster but we can still use special relativity in a consistent way to analyse what would happen if we had faster-than-light signals. (I've been deliberately avoiding the phrase "faster-than-light travel" as special relativity doesn't make sense, so far as I can see, for observers in superluminal frames.) As I've shown, if we allow FTL signals in special relativity then we can generate causal loops without a great deal of difficulty. I've said before that you can pick at most two of {special relativity, FTL, causality}. That doesn't stop you picking, in principle at least, {special relativity, FTL}, but that doesn't appear to have been the choice of the real universe. (The real universe appears to have picked neither special relativity nor FTL!)
And now little OT. When you (or anyone else) says that "in special relativity faster-than-light travel is not possible.", do people mean that any kind of movement that appears to exceed speed of light is impossible, or just the kind of movement where you follow certain path, with length s, and it takes time t so that s/t > c? Because I do not understand how causality is broken in case of wormholes. If I had an instant means to get to Alpha Centauri from earth, so that my spaceships "real" speed (traveled distance per time) is slow, even tough it seemed to travel much longer distance, how could I cause problems with causality? I do not think it can be explained with accelerating inertial frames, because I don't need to accelerate at all, I just pass through a hole with constant speed.
Well, in special relativity wormholes don't exist. To discuss wormholes we really need to get into general relativity, which is a much deeper and more sophisticated theory and one which I don't currently have time to try to explain. However, in general relativity the universe looks more and more special-relativistic as you look at ever smaller regions, and this means that material objects like spaceships can't travel faster than light in a general-relativistic universe any more than they can in a special-relativistic universe. There are, though, even more strange aspects of time and causality in general relativity. For example, it's possible for the sets 1 and 3 in my list above to overlap. This happens for spacetimes that contain closed timelike curves, which is a fancy name for paths along which objects can travel slower-than-light and find themselves in their own pasts.
It's quite easy to see how this works with a pair of wormholes in the approximation in which the wormholes are small so most of spacetime looks special-relativisitic. The key idea is that it's possible to use time dilation to "age" one mouth of a wormhole relative to the other. Suppose we have two wormholes, each with a mouth at Earth and a mouth at Alpha Centauri. We can then create a situation just like my figure 5. Suppose one wormhole is such that if you enter the Earth mouth at event P you emerge at Alpha Centauri at event Q. We can use time dilation to arrange for the second wormhole to be such that if you enter the Earth mouth at event R you emerge at Alpha Centauri at event Q. So then if you travel through the first wormhole from P to Q you can then travel through the second wormhole from Q to R (i.e. into the past). The system consisting of the pair of wormholes thus contains curves that are both timelike and closed and so collectively make up a time machine.
In fact it's possible to do pretty much the same thing with a single wormhole. Keep one mouth at Earth and send the other out on a long journey at close to the speed of light to some place far away. If you have a clock attached to the mouth that stays at home and another clock attached to the mouth that goes away then the two clocks will remain synchronised if you look through the wormhole. Suppose the journey starts in 2010AD, takes one year of proper time for the travelling mouth and finishes at an event with coordinates 2020AD and somewhere-far-away in Earth's inertial frame. In 2011 you could then step from the Earth mouth through the wormhole into 2020 in some faraway place. This is quite strange but not much of a danger to causality. However, suppose the travelling mouth makes a similar journey back to Earth. Another year of proper time elapses for the travelling mouth and it gets back to Earth in 2030. However, you could now step from Earth in 2012 to Earth in 2030, or if you're already in 2030 you could step through the wormhole in the opposite direction to get to 2012. Once again there are closed timelike curves and traditional ideas of causality must be thrown away.
[1] Philosophers would probably say that "event A causes event B" is a statement about all possible worlds in which event A and/or event B occur and would get into the concepts of causal necessity and causal sufficiency and the like. Here I'm really talking about a weaker notion of "possible cause", where "event A is a possible cause of event B" simply means that what happens at event A could influence what happens at event B.
]]> ]]>
]]>