<< Previous in Series: “Science and Truth”
In physics an event is something that takes place at a given location at a given time. This conforms closely to our everyday notion of an event. The collection of all events is called spacetime. In this series we’ll often be concerned with sets of events and their relationships to each other (especially their causal relationships). To talk more clearly about these relationships it’s often helpful for an observer to assign a unique label to each event in some region of spacetime. As space has three dimensions and there’s also a time dimension it’s possible for our observer to label an event with three numbers representing its position and one number representing the time at which it occurs. A label of this kind is called a coordinate and the collection of labels is called a coordinate system or coordinate frame.
(In special relativity it’s possible to produce coordinate systems that include every event in spacetime. This is not true when we introduce gravitation. In that case the best we can do is to cover spacetime with a set of overlapping coordinate systems that each label some region uniquely, and then translate between one coordinate system and another on the overlaps.)
Different observers will typically assign different coordinates to the same event and we’ll often consider how events labelled in one way by one observer are labelled in another way by a second observer. Coordinate systems are thus useful, but you shouldn’t read too much into them. There are deeper properties of spacetime which don’t vary from one coordinate system to another and modern physics is formulated in terms of these properties in ways which I will describe more fully as this series progresses. However, this is getting ahead of ourselves: in this installment I want to talk about a concrete procedure that an observer can use to assign coordinates using a clock and rays of light.
Firstly, we’ll need to consider the concept of spacetime diagrams, which I’ll use extensively through these articles. As I’m not sufficiently artistically skilled to draw four-dimensional diagrams I’ll restrict our view to one dimension of space as well as the time dimension. I’ll always draw the diagram so that time increases from bottom to top and space extends from left to right. Lines running from bottom to top (which don’t slope too much) are possible paths that particles can follow through spacetime. Such a line is called the worldline of the particle. It’s really a collection of events, each of which is a place and time at which the particle exists. I’ll typically plot the diagram from the point of view of an observer moving uniformly (that is, an observer who isn’t accelerating). The vertical axis will then form both the time axis and the worldline of that observer. I’ll also scale the space and time coordinates so that light rays travel at 45 degrees to the axes.
Our first problem is this: how can Alice, a uniformly moving (“inertial”) observer, decide whether or not a second observer, Bob, is at rest relative to her? She can do this using a simple method that requires only a clock and a flashlight. Alice shines flashes of light at Bob and times the interval between a flash being sent and her reception of the reflected flash, as shown in figure 1. If the interval between each flash being sent and its reflection being received is constant then Bob is at rest relative to Alice. (If each successive flash takes less time than its predecessors to get to Bob and back then Bob is moving towards Alice; if each one takes longer than its predecessors then Bob is moving away from Alice.)
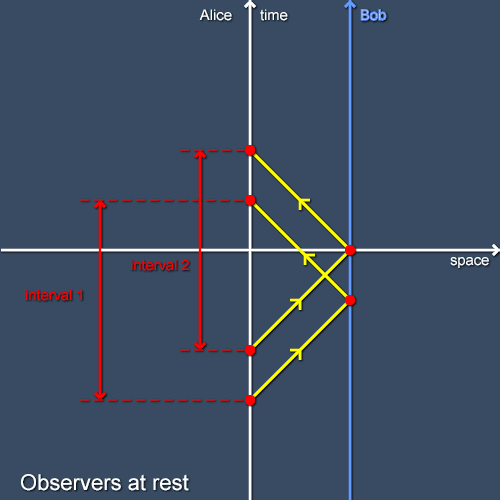
Using this same apparatus, Alice can do something even more useful: she can assign coordinates to the events at which the light pulses are reflected. The time coordinate of the reflection event is simply the average of the times on her clock at which the pulse was transmitted and its reflection received. An inspection of the diagram reveals that this is a rather intuitive definition. Giving the reflection events a spatial coordinate is a little more subtle. The spatial coordinate is proportional to the interval elapsed between the pulse being sent and its reflection received. (The constant of proportionality is half the speed of light, as the light flash has to travel twice the distance from Alice to Bob.) It should be clear that if the flash of light takes longer to return then it must have travelled further. In this case the two intervals shown are the same so the two reflection events are at the same distance from Alice, as they must be if Bob is at rest relative to her.
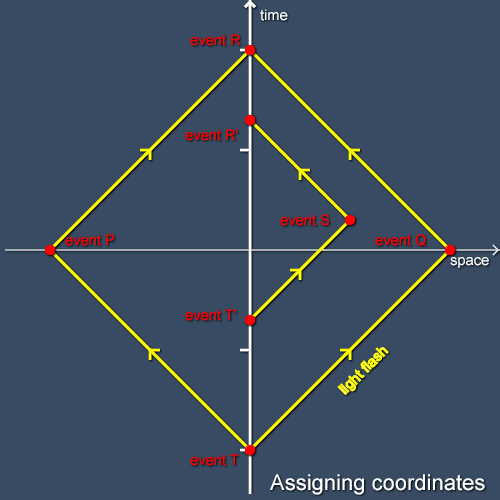
Alice can extend this process to give coordinates to all events in the (Newtonian or special-relativistic) spacetime (at least if there’s something going on at each event that reflects some of the light and she’s patient enough to wait for reflections from distant events). Figure 2 shows her using this process to assign coordinates to the events P, Q and S. To reflect pulses from events P and Q she must transmit flashes towards them from event T. She receives the reflections at event R. From this she deduces that the two events happen at the same time (in her coordinate frame but not necessarily, as we will see later, in other frames). They also happen at the same distance from her, but in different directions. From the interval between T and R she can deduce the times and distances of P and Q. She can use the same process to give coordinates to event S, this time transmitting from T’ and receiving at R’. As the interval from T’ to R’ is less than the interval from T to R, event S happens closer to her than event Q. As the average of the times at T’ and R’ is greater than the average of the times at T and R, event S happens later than event Q (in her frame). Once again, she can do detailed calculations to give S space and time coordinates. She can do the same for any other event of interest. Essentially she’s just using radar.
Given this process, Alice can lay down a coordinate grid on spacetime. Bob or any other observer moving uniformly can do likewise. However, the coordinate grids deduced by different observers will be different. As Bob is at rest relative to Alice it’s easy to translate between their coordinate systems. All we have to do is to compensate for Alice and Bob each thinking that they are at the centre of their own coordinate system, and possible make use of a simple process to synchronise their clocks to compensate for the possibility of each starting the local clock at a different time. In Newtonian physics we can also translate between coordinate systems set up by observers in uniform relative motion by using another simple and intuitive process. However, things are not quite so simple in special relativity. One of the postulates of the theory is that the speed of light is the same as measured by any inertial observer. This will have profound consequences for our coordinate translations and for many other things. In the next installment in the series I’ll extend this discussion to consider the intriguing phenomenon of the relativity of simultaneity: observers in uniform motion relative to each other will differ on their deductions concerning simultaneous events.
Next in Series: “The Relativity of Simultaneity” >>

|
Do not read the comments if you already understand the concepts. Confusion is contagious.