<< Previous in Series: “Spacetime and Coordinates”
We’ve disussed how an observer, Alice, can apply coordinates to a special-relativistic spacetime using just a clock and rays of light. Now we need to consider how things look to Bob if he’s moving with respect to Alice at uniform speed. First let’s consider two events, P and Q, that are simultaneous in Alice’s frame as shown in figure 1.
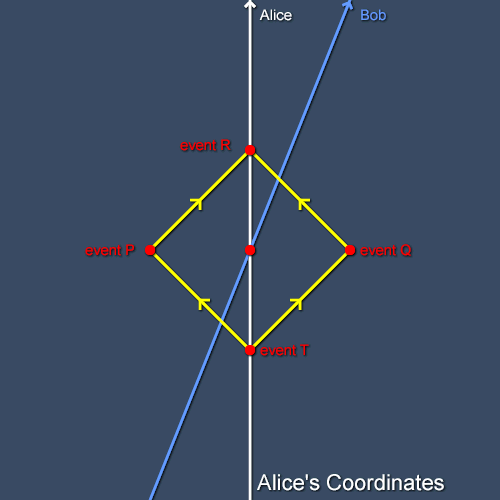
Because of the principle of relativity one inertial frame is as good as another, Bob can use the same procedure as Alice to assign coordinates to the events P and Q. Let’s watch him from Alice’s frame as he does this. To draw the diagram of this situation we’ll have to make use of the second postulate of special relativity: inertial observers always measure the same speed of light in a vacuum. This means that any light rays transmitted or received by Bob travel at 45 degrees to Alice’s coordinate axes in just the same way that any rays that Alice transmits or receives herself do. (In this sense, special relativity is simpler than non-relativistic physics, in which we’d have to concern ourselves with the possibility that light emitted by moving observers might travel more rapidly than light emitted by stationary observers.)
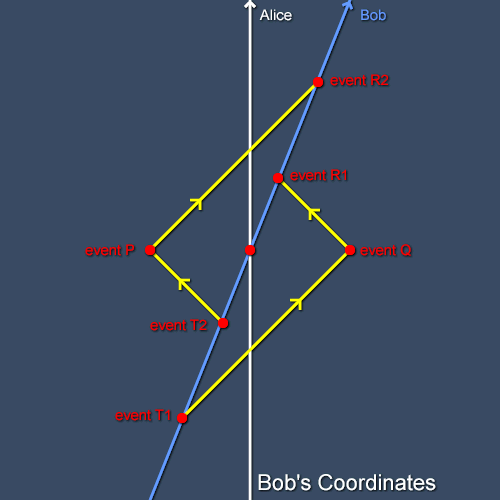
As shown in figure 2, Bob must transmit light at event T1 to bounce it off event Q and receive it back at event R1. To bounce light off event P he must transmit it at event T2 and he receives the reflection at event R2. By symmetry - a powerful tool in physics - the same interval elapses on Bob’s clock from T1 to R1 as from T2 to R2. Remember from our discussion of the method for assigning coordinates that event Q happens at the time in Bob’s frame which is the average of his times at T1 and R1 and similarly event P happens in his frame at the time which is the average of his times at T2 and R2. As the two intervals are the same and T1 is earlier than T2, it follows that event Q happens earlier than event P. This is a striking conclusion: events that are simultaneous in one inertial frame are not simultaneous in other frames. As the description in any inertial frame is as good as that in any other it follows that there is no absolute notion of simultaneity. This is the famous phenomenon of the relativity of simultaneity. It follows directly from the principle of relativity and the constancy of the speed of light.
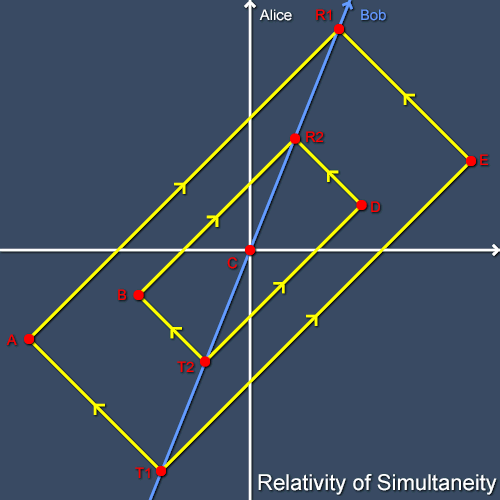
To investigate the relativity of simultaneity in more detail we must next consider the sets of events which are simultaneous in Bob’s frame. Once again we’ll watch Bob from Alice’s frame. Consider the collection of events and light rays shown in figure 3. The intervals from T1 to T2, T2 to C, C to R2 and R2 to R1 are all equal. This means that the average of the time from T1 to R1 is the time at event C, as is the average time from T2 to R2. Thus, by the procedure for assigning coordinates to events, the events A, B, C, D and E are all simultaneous in Bob’s frame (although manifestly not in Alice’s frame in which they increase in time from A to E).
Alice and Bob slice up the same spacetime into space and time in different ways because of their relative motion, and neither slicing is in any sense better than the other. (There’s nothing special about Alice’s frame; we could just as well work entirely in Bob’s frame and we’d reach the same conclusion.) This mixing of space and time is very different to the situation in pre-relativistic physics (or most people’s intuitive picture of the world) in which everyone agrees on what is space and what is time. Moreover, the experimental evidence strongly suggests that it’s a fundamental aspect of the way the world works. This won’t be the last time that our naive intuitions turn out to be a poor guide to the nature of the universe.
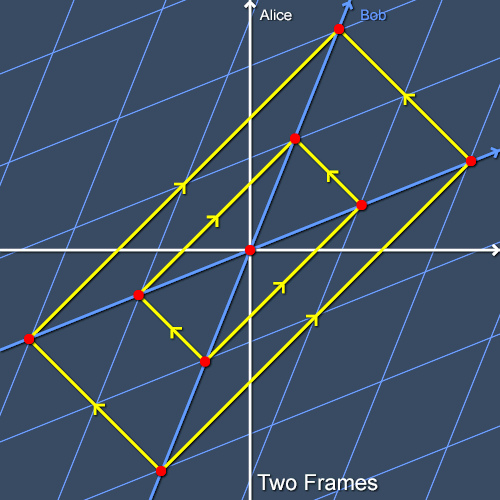
Finally, let’s draw Bob’s coordinate grid as seen from Alice’s frame. Bob’s time axis is his worldline and his space axis passes through all the events simultaneous with event C in his frame, as shown in figure 4. The other spatial gridlines of his coordinate system are all parallel with this simultaneity surface and the temporal gridlines are parallel with his worldline. Therefore, his coordinate grid is skewed as seen by Alice. (Likewise, Alice’s coordinate grid is skewed as seen by Bob.) This skewing, however, preserves the speed of light: light rays move one unit of space in one unit of time in Bob’s coordinates just as they do in Alice’s coordinates. It’s just that what constitutes a unit of space or time is different. The relationship between the two sets of coordinates is called a Lorentz transformation. We will have much more to say about these transformations later.
From the discussion so far you will no doubt have the impression that very many things have values that are only valid relative to one inertial observer or another. On pondering the relativity of simultaneity you may start to worry that the theory of special relativity has fatally undermined even such everyday notions as “past” and “future”. However, soon we’ll see that the spacetime of special relativity has its own absolute causal structure in which past and future acquire new meanings. Later we will meet various absolute quantities that have values that are independent of the state of motion of the observer. A certain solidity will thus be restored to what might now seem a disturbingly insubstantial spacetime.
Next in Series: “Absolute Future and Absolute Past” >>

|
 |
Hi John, The previous part of this series was about how Alice could attach coordinates to events in spacetime. When I say things like "how things look in Alice's frame" I mean that we should think in terms of the coordinates that Alice would assign to events using the process described in that installment. I don't mean to imply that Alice will be receiving the flashes of light used by Bob: rather, she'll be using her own flashes of light to assign coordinates to the same events but I'm not showing those flashes on the diagrams in this article or else they'd be confusing and cluttered. |

|
You don't understand how Einstein used "practical geometry" (his term for constructivist mathematics) to formulate the relativity of simultaneity, so you don't understand how he deprived the argument of logical content by saying that one point (M in the case of the train experiment) "naturally" coincides with point M'. Below is a discussion of Einstein's mathematical orientation in its historical context. Einstein is trying to avoid paradox, but if there are no paradoxes, his arguments are unmotivated. We are just starting to understand the pernicious effect of constructivism in mathematics. You are VERY far behind the times, very ignorant. I suggest you start by reading A. Garciadiego, BERTRAND RUSSELL AND THE ORIGINS OF THE SET-THEORETIC 'PARADOXES.' Then there is a good online article by Jose Ferreiros on the weird foundations of Cantor. Also, a good bibliographical essay on recent work in analytic philosophy, on her BU website. Relativity, natural mathematics, constructivism, intuitionism, blah blah blah, are all OVER. Get with with it. Search ResultsSSRN-Paradox, Natural Mathematics, Relativity and Twentieth ... Ryskamp, John Henry,Paradox, Natural Mathematics, Relativity and Twentieth-Century Ideas(June 17, 2008). Available at SSRN: http://ssrn.com/abstract=897085 ... papers.ssrn.com/sol3/papers.cfm?abstract_id=897085 - Similar pages by J Ryskamp |

|
To help me put your example into perspective, I assigned names to Alice�s and Bob�s frames. I thought about calling the frames Alice�s and Bob�s cars on intersecting roads. I settled on Earth for Alice�s frame and moon for Bob�s frame. Both frames are moving through space at different speeds and different directions relative to each other and also relative to all other moving bodies in space. I labeled you and I as remote observers residing on the surface of the sun which is also moving through space. Allice and Bob and you and I have all the same information you show in your diagrams. Now with all those labels, we look at your diagrams. Event T on earth begins a trip for a flash of light. Events P and Q are reflections on earth that are simultaneous. Event R is the joining of the two simultaneous reflections. That make event R represent another simultaneous event. This is similar to any and all measurements of the speed of light on earth, in Alice�s frame. Regardless of where on earth or when on earth, the speed of light is always the same and a round trip always measures the same distance between equally spaced objects on earth. The same conditions described for earth also apply to the moon. When bob looks at the events on earth, he sees a moving earth and the points on earth are fixed relative to earth but moving relative to the moon as well as moving relative to you and I on the sun. Bob and you and I see point T on earth when the flash first occurred. We also see point T in space. The earth moves from point T in space. Alice and Bob and you and I know that the earth and moon and sun are moving in space and time. Although Alice observes the simultaneous events at P and Q, Bob and you and I know that our observance is a false perception because we know all the facts. Using all the data, we calculate the different perceived arrival times and concur that the events are in fact simultaneous. The same conditions apply when Alice and you and I observe the same series of events on the moon. Remember, Allice and Bob and you and I have all the same information you show in your diagrams. We all know about your diagram with different start times and perception instead of the facts. We know that we must make calculations to adjust for false perception. Nothing in your diagram precludes inclusion of the facts that we all know. We have different perspectives of events but we also have the ability to collect data and include that data in our calculations to show different begin and end times as well as the fact that simultaneous events are simultaneous regardless of the frame of reference where the observer resides. |

|
Very clear illustration of the relativity of simultaneity, demonstrating the concept with easy to read diagrams. What I would like to see is the frequently used train example, but with what observers would see( aboard the train as well as on the tracks). For instance, the case where two bolts of lightning are fired simultaneously (from the track observer's perspective) at two points on the track is often used. The illustrations are quite good at showing that the track observers deduces that the lightning strikes are simultaneous from his perspective while the train observer deduces that the lightning strike at the front of the train occured earlier than the one at the back of the train. However, what is hard to find is what both observers would actually see |
Dear Richard,
Sorry, I do not understand what you mean when you say that you view what Bob is doing from Alice's frame.
What does Alice actually view? In figures 2, 3 and 4 all you show is the light transmitted and received by Bob. Nothing that is received by Alice.
So how can we view it from her frame of reference?
Maybe I am missing something. Would appreciate if you could clarify.
Many thanks, John.