A commenter writing about my earlier post, “Relativity, FTL and Causality” said:
As far as FTL being equivalent to time travel, the above explanation is correct. As far as FTL being impossible at present, it is not quite. Richard’s explanation lacks a mention of black holes. An object (with non-zero mass), falling into a black hole from rest, will cross the event horizon AT THE SPEED OF LIGHT. Unfortunately we (the distant observers) would not be able to witness this event, since the falling observer would take forever (from our viewpoint) to reach the event horizon. In the falling observer’s reference frame, however, he’d be flying at the speed of light all right! Moreover, he’d probably be able to time travel as well, as his speed continues to increase (to >c) inside the event horizon. Whether this would lead to any causality violations is unknown, since we can’t see past the event horizon, and the unfortunate falling observer has a short time to live before he hits singularity, causality violations or not. However, from a purely theoretical point of view, we know that FTL travel is possible with black holes.
This comment about black holes is not true, at least in general relativity, the relativistic theory of gravity. It’s correct that the radial velocity of an infalling object goes to zero at the event horizon when expressed in the coordinates of an inertial observer who is stationary with respect to the black hole and far away from it. In other words, the distant observer sees the falling object approach the horizon but never cross it. However, if a second observer falls in a windowless[1] spaceship she would notice nothing out of the ordinary, except for tidal effects, as she crosses the event horizon. If the tidal effects are sufficiently small (they can be made arbitrarily small by increasing the mass of the black hole) then she’d have no way of knowing whether she was falling into a black hole or just drifting through space. This is one aspect of a general feature of general relativistic spacetimes: as the region considered gets smaller and smaller it looks more and more like the spacetime of special relativity. Moreover, there’s no frame in which her trajectory becomes spacelike so she can’t be said to be travelling faster than light.
On the other hand, there’s clearly something special about the event horizon of a black hole, and the singularity in its interior. What happens in a black hole spacetime is that the light cones near the black hole are “tilted” compared with what a naive observer at far away from the hole might expect. At the event horizon the tilting becomes so great that there are no future timelike or lightlike trajectories that can escape to infinity. The singularity is therefore not really at the “centre” of the black hole - although it looks that way in the coordinate system of the distant inertial observer - but rather in the future of all observers who fall across the horizon. And typically, and unfortunately for our daring black-hole explorer, not that far in the future.
One way to visualise this is through the use of Penrose diagrams. These are diagrams of the causal structure of a spacetime in which the points infinitely far away in space or time have been drawn at finite distances on the diagram through the use of a “conformal mapping” that leaves the causal structure intact. (The conformal mapping distorts the geometry of the spacetime to more clearly show its causal structure.) Rays of light in these diagrams still travel at 45 degrees to the vertical as in all of my Minkowski diagrams. The edges of the diagram are then the regions of timelike, spacelike and lightlike infinity - and singularities at a finite distance. This all sounds rather arcane, so let’s look at an example:
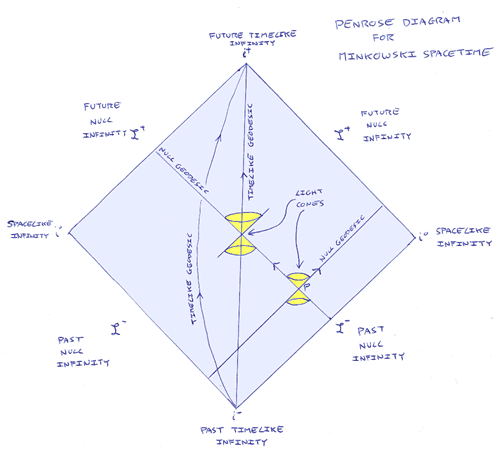
On this diagram I’ve shown two possible paths for freely falling observers. (These paths are technically called “timelike geodesics”.). Just as in my other diagrams of spacetime, at each event along the timelike path the path itself is in the light cone of the event, so all observers with mass travel slower than light. If we follow either of the two example paths - or indeed any timelike geodesic - forward in time we reach the region called “future timelike infinity”. If we follow them backwards in time we reach “past timelike infinity”. Similarly, light rays can shine from “past null infinity” and can extend in the future to “future null infinity”. As we might expect, all the edges of this diagram are the appropriate kinds of infinity as Minkowski spacetime extends infinitely in space and time from any given event.
Now let’s take a look at the causal structure of a spacetime that contains a spherical, uncharged, non-rotating star collapsing to form a black hole. (The spacetime for an eternally existing black hole has features I don’t wish to discuss here.) In this case the spacetime outside the star isn’t a Minkowski spacetime but a Schwarzschild spacetime. However, causally - and remember that Penrose diagrams show only the causal structure and not the geometry - the outside region is very much like Minkowski spacetime. The inside is very different though.
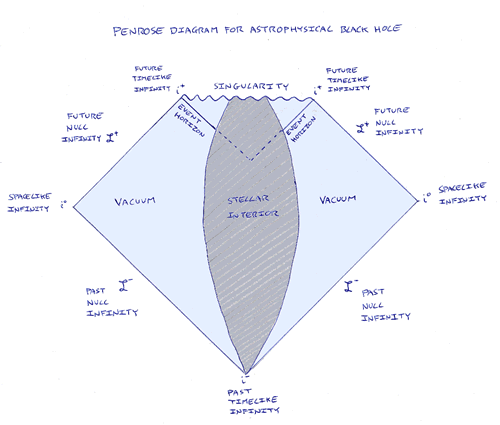
Once again, outgoing light rays originating from anywhere in the exterior vacuum region can reach future null infinity and (some) freely falling matter particles can reach future timelike infinity. But the diagram clearly shows that a light ray or matter particle from the region inside the event horizon of the black hole cannot reach future null or timelike infinity respectively. No matter in which direction or at what speed particles inside the horizon move, they can only ever reach the singularity. The singularity itself is a spacelike hypersurface on which all world-lines passing through the event horizon terminate. To escape from it, one would have to be able to travel faster than light. Otherwise it is, very literally, the end of time.
[1] If she were fortunate(?) enough to have windows to observe the outside world she’d see some strange things that I won’t discuss here.

|

|
Hmmm. It seems to me that there is a contradiction here. The event horizon, by definition, is a surface where the escape velocity reaches the speed of light. Therefore, it would seem logical that an infalling object would reach the speed of light at that point. Maybe the problem lies in the fact that it's difficult to measure the speed of the falling observer. Speed can only be measured locally, and there can be no stationary observers on the event horizon. From a physical point of view, however, it makes perfect sense that the observer reaches the speed of light at the horizon: if he didn't, he could've escaped with a sufficiently powerful rocket engine. Now as far as what goes in inside the event horizon. We might not be able to test this experimentally for a while, but it seems to me that the observer should continue to accelerate once "inside". Tidal forces are not a problem for a sufficiently massive black hole, and the time to hit singularity can be arbitrarily large. Does it mean that a superluminal movement can be reached? You said in your explanation, "To escape from it [singularity], one would have to be able to travel faster than light". That seems to imply that you ARE traveling faster than light when you're in a free fall. The physical meaning, however, is tricky. As you point out, singularity is not a point in space but "the end of time". However, this is consistent with your relativity post. Once moving faster than light, you're no longer just traveling in space but rather in time. The current black hole theories predict that inside the event horizon, time becomes "spacelike" and space "timelike". I haven't been able to find anybody who could attach a physical meaning to this, but it seems to me that it's like this: your motion in space is now constrained (you cannot escape getting closer to singularity), but you have some freedom to move in time! Just the opposite of what you normally experience, of course. So, causality violations may or may not be possible. Maybe you're able to move in time, but only in a self-consistent way (no paradoxes). Whichever way you look at it, IMHO, 1) Inside the event horizon, you HAVE to be moving faster than light (because the escape velocity is greater than c; 2) It does not lead to physical contradictions because FTL=time travel, but you ARE in effect time traveling (time and space change places) (whether it leads to philosophical contradictions is another matter...); 3) For now, the Universe is safe for historians, because "what happens in the EH, stays in the EH". |

|
There are indeed other black hole solutions to the field equations: the Reissner-Nordstrom for charged black holes and the Kerr solution for rotating black holes. Both have even more exotic causal structures, with such interesting aspects as multiple asymptotically flat external regions, timelike rather than spacelike singularities, and even closed timelike curves inside the horizon. I'm somewhat reluctant to promise future installments to make this a series on the causal structure of spacetimes - both because it's a digression from my main series on physics (which is itself stalled) and because Sharp Blue is littered with other stalled series awaiting future installments - but I may write more about these things and about the causal structure of open and closed universes at some point in the future. |

|
Maybe that's how it's defined in popular science articles, but general relativists don't use that definition. A spacetime contains a black hole if it contains a "black hole region" that is not in the causal past of future null infinity. The event horizon is the boundary of this black hole region. As you say, you can only measure speeds locally in any physically meaningful way in a curved spacetime like that of a black hole. An observer at any event in a general relativistic spacetime will measure the speed of any object passing through that event to be less than the speed of light. However, there's no good way to compare velocities measured at different events. This is one key difference between special and general relativity. To compare two velocities - or other vectors or tensors - measured at two different events, you need to "carry" one from the event at which it was measured to the event at which the other was measured. To do this, you need to use a mathematical gadget called the Levi-Civita connection (which depends on the geometry of the spacetime) and to specify a path between the two events. The value of the comparison depends on the path chosen, and there's nothing in general relativity that picks out any preferred paths. (Aside 1: In special relativity the connection is such that the value of the comparison doesn't depend on the path taken. This is equivalent to saying that Minkowski spacetime is "flat".) (Aside 2: connections are ubiquitous in physics, as are "curvatures", which describe what happens when one carries an object around an infinitesimal loop. The connections and curvatures don't have to describe the geometry of a spacetime but can describe the geometry of a "bundle over spacetime". For example, the electromagnetic potential and the electromagnetic field are the connection and curvature used to carry a certain kind of "phase" around in spacetime.) In any case, the key point is that once you've crossed the horizon you can accelerate all you like in any direction you like and you still won't be able to avoid the singularity. (The only way you can do so is to travel along a spacelike path, which probably isn't possible and certainly isn't possible using rocket engines.)
It's not actually true that time becomes spacelike and space timelike inside the horizon. This is just a misunderstanding caused by one of the usual ways to draw lightcones on a spacetime diagram and a failure to use the connection to make comparisons properly. At every event in the black hole spacetime there are three spacelike dimensions and one timelike dimension, and nothing weird happens to the spacelike or timelike character of the dimensions as one crosses the horizon. In particular, an observer travelling along a timelike path towards the horizon will still be travelling along a timelike path on and within the horizon. It's partly to try to explain this that I've drawn these Penrose diagrams rather than any of the more familiar kinds of spacetime diagrams. The Penrose diagrams may distort the geometry but they preserve the causal structure and have the virtue that the "up" direction is always timelike and the "across" direction always spacelike. |

|
I read with interest your articles on FTL travel & the fact that only 2 of the 3 (FTL, Special relativity & causality) can be true, but I wonder can you explain what the loss of causality would mean in how the universe operates? |
What about a Kerr Black Hole? I read somewhere that unlike the Scharwzschild Black Hole that has, supposedly, a pin point singularity at its core, the Kerr Black Hole seems to have neutrons in a ring effect as the singularity. Essentially it gives the effect that something could pass through the singularity and essentially into another dimension, time, etc.
This idea from the Kerr Black Hole strikes similarly to what I suggested for my TDA portal formation, although mine was completely make believe. Maybe it wasn't too far off. A spiraling ring of neutrinos, radiated with Tachyon emissions and the presence of a massless luxon that allows for the portal to form and essentially propel someone or something faster than light to another time.
I've also heard of something called a naked singularity. It holds the same principles as that of a Kerr Black Hole, but there is no event horizon or gravitational force. It is like an invisible ring in space. However, this ring could become visible because it has no event horizon, making it observable. This sounds exactly like my portal in my book that the scientists create. I basically set it up as a small slit that begins expanding in a circular frame to reveal the other time on the other side, pulling the two time frames together. I also read that these can possibly emit light, which is reflected in the fact that my rogue time traveler at times experiences a great, white light as they proceed from one time to another with his cylindrical device that I'm calling a Collider (named after the LHC, kind of an homage).
All of this started coming to me after I just made mention of the portal being a small black hole. When I saw a television special about primordial black holes, I began to realize, not having a scientific background, I wasn't that far off the mark after all. Black holes defy the laws of physics, so it would only make since that if we ever find a way to travel through time, or even faster than light, somehow a black hole might play into that equation one day.
Recently in the news I saw that researches have found the smallest black hole ever recorded, only 15 miles wide. Then I saw the story of the massive void in space, 1 billion light years wide. It's amazing to me how vast and limitless this universe is, but how much it is only the tip of the iceberg in relation to what is going on in the cosmos. I believe one day we'll not only travel faster than light or through time, but between universes as well, in a multiverse that will one day unite all realities as one. Perhaps black holes or "cold spots" in the universe will have something to do with that, when we have the technology to handle it.
Until then, I'll just keep writing my stories and encorporating the physics needed to make it seem real!