In the previous part of what has now become an ongoing series on the causal structure of various general relativistic spacetimes, I discussed the causal structure of the flat, Minkowski spacetime of special relativity, and of the Schwarzschild vacuum outside a spherical, uncharged, non-rotating star which collapses to form a black hole. In this part, I’d like to discuss the so-called Kruskal extension of the Schwarzschild vacuum. This is the general solution for a static, asymptotically flat vacuum (that is, a matter-free spacetime that looks like Minkowski spacetime when one is far away from the event horizon) containing a black hole. In other words, this time we’ll consider a black hole that exists for all time, rather than one which forms from the collapse of a star.
As commenters have noted, the astrophysical black hole in the last article is not a time-symmetric solution as there’s a star early in time and a black hole late in time. The time reverse of this solution is a “white hole”, from which matter can emerge into the outside universe but into which no matter can fall. The Kruskal extension of the Schwarzschild metric is time symmetric and it contains both a black hole region and a white hole region (and is thus occasionally called a “grey hole”). The former contains a singularity that is in the future of some lightlike and timelike paths - those that enter the black hole - but in the past of none. Similarly, the latter contains a singularity that is in the past of some lightlike and timelike paths but in the future of none. More surprisingly, the full solution contains two asymptotically flat external regions, each of which is causally isolated from the other!
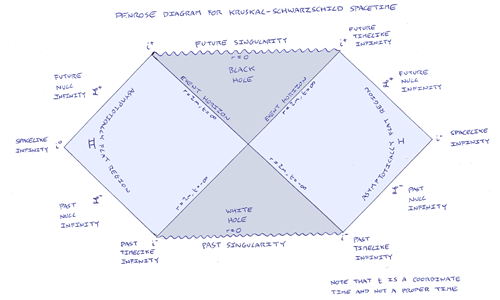
Even though these posts are about the causal structure of the spacetimes in question rather than their geometries, I feel that at this point I ought to say something more about coordinates I’ve used in this diagram. For observers at rest with respect to the hole and far away from it in one of the asymptotically flat regions, the t coordinate is just proper time as measured on a standard clock. Suppose this distant clock emits a regular “time signal”: a flash of light to mark every second of its proper time. An observer elsewhere in the external vacuum who is at rest with respect to the distant clock will not in general receive one time signal flash per second of her proper time. If she’s closer to the hole then she’ll receive more than one flash per second as measured on her clock. (If she emits her own time signal flash once per second of her proper time, the distant clock will receive them less often than once per second of its proper time. This is the famous phenomenon of gravitational time dilation, which leads immediately to gravitational redshifts and blueshifts. Unlike the time dilation of special relativity its not symmetric with respect to the two clocks.) However, by adjusting the mechanism of her clock so it runs more slowly she can make it tick in synchrony with the time signals arriving from the asymptotically flat region. In this way - provided a timelike hypersurface is chosen as a “zero” of coordinate time - the t coordinate can be extended across the external region.
The r coordinate is much easier to grasp. It’s a radial coordinate with respect to the hole that’s chosen such that a sphere of constant r coordinate has an area of 4 pi r^2. (Every point in the Penrose diagram is such a sphere at a certain time.) Note, though, that this means that r is not a proper distance (that is, a distance measured by using measuring rods). As the spacetime is spherically symmetric it’s easy enough to finish off our coordinate system by picking two angular coordinates, but these won’t concern us here.
The event horizon of the hole is at an r coordinate of 2m (where m is the mass of the hole and I’m using coordinates in which the gravitational constant and the speed of light are both equal to 1). (This distance is called the Schwarzschild radius, but it’s not, of course, a proper radius.) As I described in the last part, a distant observer watching an object fall into the black hole sees it fall ever more slowly towards the horizon (and at the same time it appears to get ever more redshifted and ever dimmer). The black hole’s event horizon is thus at a t coordinate of +infinity. (Remember, though, that the falling object crosses the event horizon in a finite amount of its proper time.) In a similar way, the distant observer sees any objects that emerge from the white hole as having done so infinitely long ago in coordinate time. The white hole’s event horizon is thus at a t coordinate of -infinity.
At some future time, I’d like to say something about the causal structure of rotating and/or electrically charged black holes, but in the next part of the series I’m going to focus on the causal structure of open and closed universes.

|
Black holes are the result of believing that bodies move by gravitational geodesic. The first and second array element of the Schwarzschild metric are the mathematical inverse of each other. But if they were equal, then, even independently of the possible zeros and infinite, light cones never be closed. There would be no event horizons or black holes.
Connected theory, the only alternative to Einstein's general relativity, is the solution to the problems of theoretical physics today. See Bubok.com:
http://www.bubok.com/libros/6346/Extracto-de-la-Teoria-Conectada
The solution to the problem of dark matter in the following link:
http://vixra.org/abs/1002.0007
Xavier Terri