Sharp Blue: Time dilation

<< Previous in Series: “Relativity, FTL and Causality”

In special relativity, time as measured by a clock is called proper time. This is the only time that is invariant. An observer, Alice, in an inertial frame can use the time as measured by a clock that she is carrying to construct a coordinate time that assigns a unique coordinate time to every event, simply by labelling each event that is simultaneous with her clock ticks with the elapsed time as measured by the clock. For the sake of definiteness, let’s say that Alice’s clock ticks once a second.

However, as described in the first part of this series, “Relativity, FTL and Causality”, another observer, Bob, in uniform motion with respect to Alice will have a different notion of simultaneity. This means that if he similarly constructs a coordinate system then he will assign different coordinate times to each event to those assigned by Alice. (And, of course, our two observers will assign different position coordinates too!). The recipe for translating the coordinates used by the two observers in different inertial frames is given by a Lorentz transformation.

Figure 1 Alice and Bob, who are moving with respect to each other at 0.4c, have coordinate systems for spacetime that are “tilted” with respect to each other. The two observers synchronise their clocks as they fly past each other at event P.

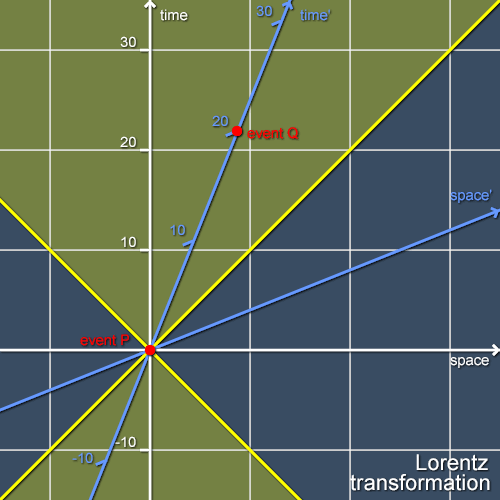
Now, this is a particularly complicated diagram and so it’s perhaps a good idea to study it more closely. Consider event Q. This is the event at which Bob’s clock ticks for the twentieth time. Both Alice and Bob agree that Bob’s clock has ticked twenty times between event P and event Q - how could they not? However, they also disagree over the time at which Q occurs (and so, in a sense, over whether Bob’s clock is really measuring time). Let us first look at things in Alice’s frame:

Figure 2 Alice considers that event Q occurs when her own clock has ticked more than twenty times.

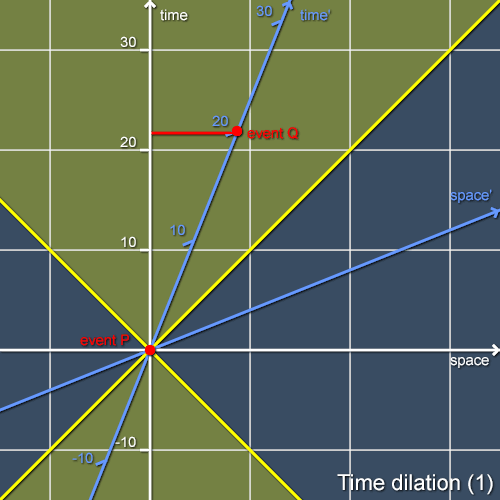
Alice finds the coordinate time of event Q by seeing which of her simultaneity surfaces it lies upon (the relevant portion of this surface is shown in red in Figure 2). She observes that that Q happens on the simultaneity surface that passes through the interval between her own clock’s twenty-first and twenty-second tick. To be precise, it happens at a coordinate time in her frame of 21.8s after she and Bob synchronised their clocks. Alice is forced to conclude that there is something odd about Bob’s clock - if it is showing 20s when she knows that 21.8s have elapsed then it must be running slowly. As this is true for any type of clock that Alice and Bob might choose, it is reasonable to say that time itself must be running more slowly for Bob (indeed at only 92% of the rate as measured by Alice [this factor obviously depends on the observers’ relative speed]). This is time dilation, one of the most famous consequences of special relativity. Alice shudders, and is glad that she’s not flying around in spaceships at high speed and suffering such odd effects.

Bob, however, sees things differently. He knows that his clock and his time are perfectly fine, thank you very much. Instead, something very odd is happening with Alice. Here’s how things look from his point of view:

Figure 3 Bob considers that event Q occurs when Alice’s clock has ticked fewer than twenty times. (Remember that for consistency we’re drawing Bob’s coordinate grid in Alice’s frame. We could equally well make Bob’s axes vertical and horizontal, in which case Alice’s would be tilted the other way.)

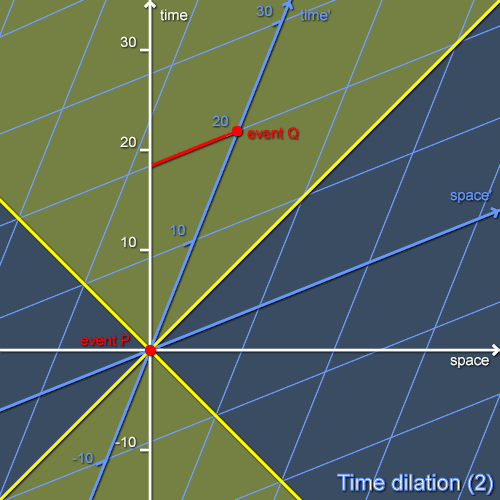
Bob uses the same procedure as Alice (but using his own simultaneity surfaces) to construct a coordinate system. He finds that event Q happens at the same time as Alice’s clock is between its eighteenth and nineteenth ticks. Bob thus considers that when 20s have elapsed since he and Alice synchronised their clocks, Alice’s clock has ticked somewhat fewer than twenty times. As this is true for any type of clocks that he and Alice might choose, he concludes that time for Alice must be running more slowly than for him - indeed at only 92% of his rate.

This is a quite peculiar situation - both Alice and Bob consider the other’s time to be running at only 92% of the “right” speed. This is a general phenomenon. Pairs of observers in uniform relative motion will each consider the other’s time to be running slowly. Indeed, because the Principle of Relativity says that any inertial frame is as good as any other, it’s meaningless to ask which is the “real” progress of time. It’s only when people carry clocks along two different paths between a pair of events that they can compare their elapsed proper times in a physically meaningful way. I’ll describe the further strange consequences of time dilation in a future article about the Twins “Paradox”.

Next in Series: “Length Contraction” >>