Sharp Blue: Length contraction

<< Previous in Series: “Time Dilation”

The theory of special relativity revolutionised not just our understanding of time but our understanding of space too. I have already described the phenomenon of time dilation, whereby pairs of clocks in uniform relative motion each tick more slowly with respect to the other. A closely related effect is the phenomenon of length contraction (sometimes known as “Lorentz contraction”, “FitzGerald contraction” or even “Lorentz-FitzGerald contraction” after the physicists who predicted it on the basis of a crude forerunner of special relativity). Both time dilation and length contraction are immediate consequences of the Lorentz transformation (which I described in my article Relativity, FTL and Causality), and hence an essential part of any relativistic understanding of the world.

Let’s see in detail how length contraction arises from the Lorentz transformation. Length contraction is an effect that applies to any moving object, but it’s easiest to consider the case of a one-dimensional rod (this follows the grand tradition in physics of ignoring any details which are extraneous to the explanation!). Consider such a rod flying at great speed past Alice, who remains stationary:

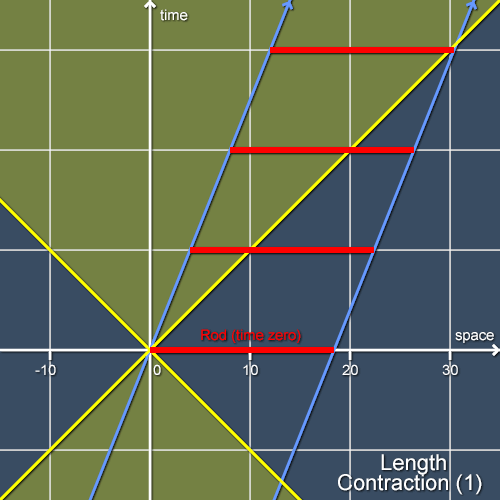
The method that Alice uses to measure the length of the rod is quite straightforward. She waits for the back of the rod to pass her and notes where the front of the rod was at the same time (to do this, of course, Alice has to set up a coordinate grid in some manner; I’ll describe in a future article how she might do so). When Alice knows where the front and back of the rod were at the same time then working out the length of the rod is easy: she just uses a ruler to measure the distance between those two locations. In the example in figure 1, she’d find the length of the rod to be a little over 18 units.

Now, if you’ve been paying attention to this series, you’ll be able to see trouble coming. For Alice to be able to measure the length of the rod like this, she has to have a notion of simultaneity, and as I’ve already discused there is no observer-independent way to say which two events (that take place at different locations!) are simultaneous. To see this more clearly, let’s consider how things look from the point of Bob, who is foolhardy enough to ride along on the rod as it races past Alice. Bob measures the length of the rod relative to his (and the rod’s) coordinate frame simply by laying out his ruler along the rod and reading off its length:

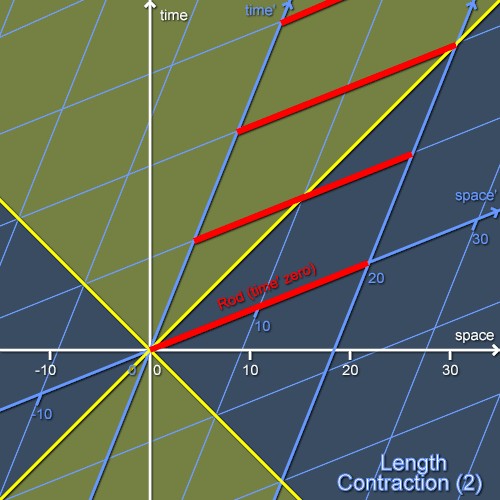
Notice that something curious has happened: as measured by Bob the rod is exactly 20 units long. Alice and Bob thus see the rod as having different lengths! The shortening of the moving rod as seen by Alice is length contraction. People in other frames will measure yet other lengths. Each person will consider all the others to be measuring the positions of the front and back of the rod at the wrong times too! However, there’s one frame that has a special value for the length. This is Bob’s frame, the frame in which the rod appears to be at rest. The length measured in this frame is called the proper length of the rod and is the closest thing in a relativistic world to our classical notion of length. Just as the proper time is the time that’s inherent to a clock so the proper length is the length that’s inherent to a rod.

If you look at a clock moving past at constant speed you’ll see it both contracted along its direction of motion and running slowly. The factor by which it contracts is the reciprocal of the factor by which it runs slow: if each tick takes twice as long as you’d expect for a clock at rest then the clock looks like it’s shrunk by half along its direction of motion. (The lengths transverse to the motion are not affected.) And, as I’ve said, all other objects will be affected similarly. This means that length contraction and time dilation are not just the peculiar behaviour of specific types of clocks or measuring rods but really properties of the ways that different observers carve spacetime into space and time.

(If you’ve really been paying attention, you’ll notice that I’ve glossed over an important point for the sake of brevity. If Bob were to look at an object in Alice’s frame then he’d see it contracted by just the same factor as she sees objects in his frame contracted. This must be so or else we’d have violated the principle of relativity. It’s this symmetry between the two frames of reference that, together with the constancy of the speed of light, pins down the exact amount of length contraction. If you find this glib explanation unsatisfying, I can only say that for the moment my angle in these articles is working out consequences of the Lorentz transformation. Later, I will explain in more detail how Lorentz transformations arise from the two postulates of the theory.)