<< Previous Article: “The relativity of simultaneity”
In the last installment we saw that observers in different inertial frames (each of which is moving with respect to the others at a uniform velocity) will consider different sets of events to be simultaneous. It’s as if the various inertial observers have space and time axes that are tilted with respect to those of the other observers. This is very unlike the situation in Newtonian physics, in which all observers agree on simultaneity. In this installment we’ll investigate the consequences of the relativity of simultaneity in more detail, focusing on its implications for the ideas of past and future.
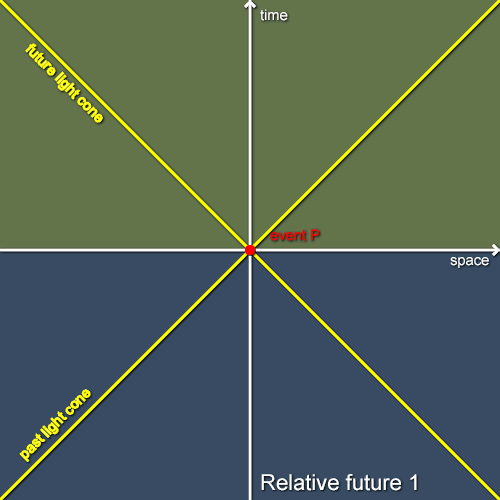
Firstly, let’s consider a single inertial observer, Alice, and an event P that’s at the origin of the coordinates in her frame as shown in figure 1. In this diagram I’ve shaded all the events that Alice considers to take place later than P. As we might expect, these are the events with time coordinates in Alice’s frame that are greater than the time coordinates of the events that Alice considers to be simultaneous with P (in other words, the events that are above Alice’s space axis). It’s not standard terminology but we might consider these events to make up the relative future of P in Alice’s frame. Similarly, the unshaded events below Alice’s space axis make up the relative past of P in her frame. (If we were considering Newtonian physics, that’s all that we’d have to say about this as past and future would be not relative but absolute.)
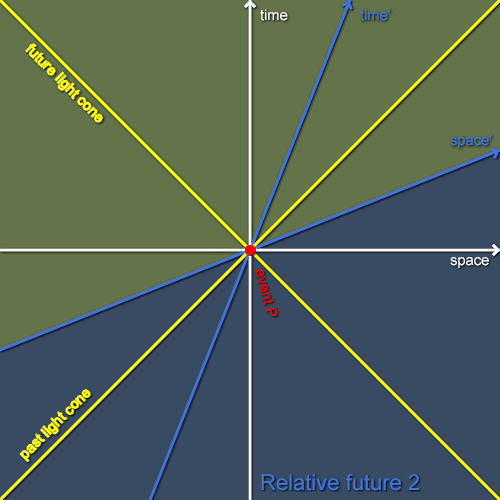
Next, let’s consider the situation as seen by Bob, who is flying past Alice at a constant speed in the positive x direction. As usual, in figure 2 I’ve chosen to draw Bob’s axes in Alice’s coordinates so we can easily compare the situations of our various inertial observers but there’s nothing special about Alice’s frame and we might just have easily drawn things in his coordinates instead. As previously described, Bob’s space and time axes are tilted towards the light cones with respect to Alice’s in such a way that he sees the same speed of light as Alice does. As Bob considers a different set of events to be simultaneous with P, the relative past and future of P in Bob’s frame will contain different events to its relative past and future in Alice’s frame. Once again, I’ve shaded the relative future of P in Bob’s frame. Quite a lot of the events in the future of P relative to Alice are also in its future relative to Bob. However, Alice and Bob also disagree about two “wedges” of events: those taking place between their respective space axes. Alice considers the wedge in the positive spatial direction to be in P’s future but to Bob they’re in P’s past. Similarly, Alice considers the wedge in the negative spatial direction to be in P’s past but to Bob they’re in P’s future.
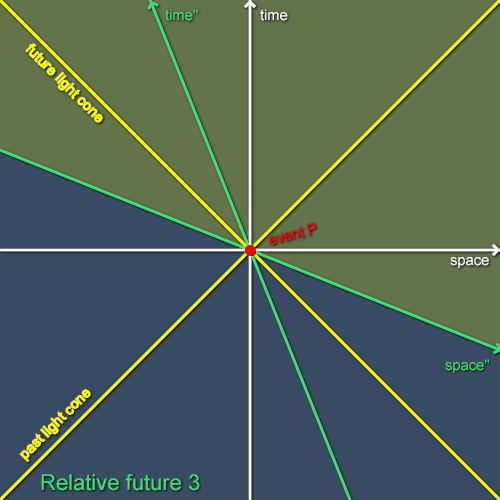
If we recruit Carol to fly past P at a constant speed in Alice’s negative spatial direction then we see the situation in figure 3. As expected, Carol’s axes are tilted with respect to Alice’s (and Bob’s, although Bob is not shown). Once again, I’ve shaded the relative future of P with respect to Carol. The situation is very like the previous one we’ve considered, with Alice and Carol disagreeing on two wedges of events. You might like to imagine the situation of Carol as seen by Bob or vice versa: they too will disagree about two wedges of events. When we consider all three of our observers, they will disagree about even more events, but notice that there will still be some events that they all agree happen later than P and some that they all agree happen earlier than P.
Finally, consider a whole family of inertial observers moving at a range of velocities with respect to each other, as shown in figure 4. To reduce clutter I’ve only shown the spatial axes of the observers, but you should be able to imagine the time axes too without much difficulty. For each observer I’ve shaded the events in the relative future of P in his or her frame, and I’ve overlaid all of these different relative futures. The more saturated the yellow at an event, the more of our family of observers agree that it occurs later than P. As we consider inertial observers that move ever faster (but never faster than light) we must consider spatial axes that tilt ever closer to the light cones (which are the paths taken by light rays) but never cross them. This means that all inertial observers agree that the events within the future light cone through P occur later than P. This region, shown in saturated yellow on the diagram, is the absolute future of P. Similarly, all of our observers agreee that all events in the region within the past light cone of P occur earlier than P. These events, shown in dark blue, make up P’s absolute past.
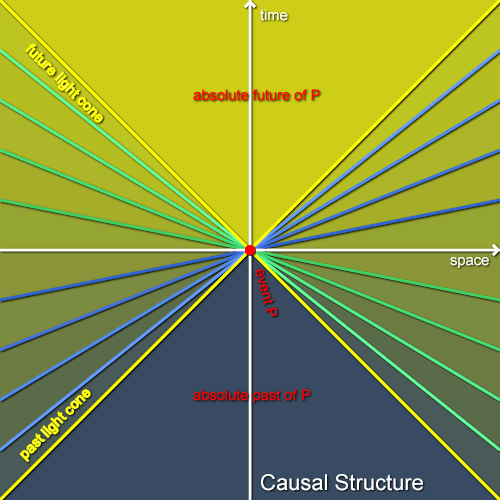
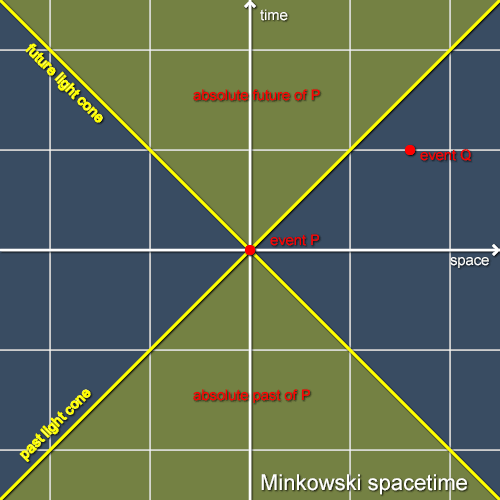
We can analyse any event in the special-relativistic spacetime (“Minkowski spacetime”) in the same way, so each event has an absolute past and an absolute future (but not the same absolute pasts and futures!). The light cones through each event and the absolute pasts and futures form a sort of “causal grain” that runs through spacetime, and are the absolute structures in special-relativistic spacetime that conceptually “replace” the absolute simultaneities of Newtonian physics. Structures such as the absolute pasts or futures which are agreed upon by all inertial observers are called Lorentz invariants. These are extremely important in relativistic physics. Figure 5 shows the past and future light cones and the absolute past and future of an event P in Minkowski spacetime stripped of clutter (the white lines are Alice’s coordinate grid). Notice that there are events such as Q that are in neither P’s absolute future nor P’s absolute past. For such events there will be some inertial observer for whom P and Q are simultaneous.
We have now learned quite a lot about space and time in special relativity. In the next few installments we will investigate some of the more striking consequences of the theory. First we will consider the way in which faster than light signals would cause violations of causality (fortunately for causality but unfortunately for our science-fictional dreams there are no known phenomena which allow faster than light signalling). Then we will look in more detail at the phenomena of time dilation and length contraction, before moving on to the celebrated “twins paradox” (which will turn out to be not so paradoxical after all).
Leave a comment